数学的浩瀚海洋中,极限的概念无疑是一颗璀璨的明珠。它不仅是分析学的基石,更现代科学和工程领域中扮演着不可或缺的角色。研究极限的过程中,有一种现象常常引发无数争议与思考,那就是“极限不存”。本文将探讨极限不存的原因、影响以及其数学及物理学中的应用。
极限不存的原因
探讨极限的过程中,“极限不存”的情况往往源于几个典型的原因。当一个函数某一点的周围没有趋向于某个固定的数值时,极限便会被认为不存。例如,考虑函数(x) = sin(1/x)(当x趋向于0时)。由于sin(1/x)接近0时震荡剧烈,我们多么靠近0,这个函数的值都没有趋向于某个确定的数,由此可见,极限此点上是不存的。
某些情况下,我们可能会遇到极限趋向于无穷大或负无穷大的情况。这并不是极限不存,而是需要更深入的理解。例如,函数(x) = 1/x,当x趋向于0时,(x)的极限并不为某个实数,而是趋向于正无穷(当x从正侧接近0)或负无穷(当x从负侧接近0)。这种情形下,数学家们将其称为“无界”,而极限的形式则被认为是不存的。
极限不存的影响
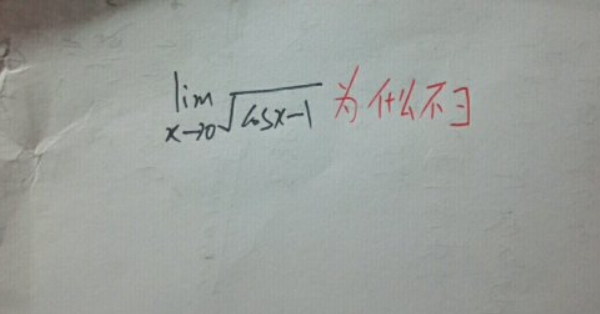
极限不存的现象数学上并不仅仅是一个技术问题,它往往能揭示出函数的性质和行为。例如,动态系统和混沌理论中,许多函数的行为某些点上是不可预测的,这实际上反映了系统的复杂性。科学家和工程师们正是这样的不确定性,研究岌岌可危的系统状态,并尝试微小的变化来预测结果。由此可见,极限不存表面上似乎是一种“失败”,但却常常是深刻理解系统动态的切入点。
物理学中,尤其量子力学与相对论的研究中,极限的存与否也扮演着重要角色。例如,描述黑洞的特性时,物理学家们发现引力场黑洞边缘表现出极限不存的特征,即事件视界附近,时间与空间的规律发生极大扭曲。此时,传统的“极限”中寻找解的思维模式可能无法得出有效的,反而可能促使我们重新审视现代物理学的基础。
超越极限的思考
当我们认识到极限不存的现象时,也许是时候换个角度看待这一概念。极限的“不存”并非是失败的象征,而是对我们认识世界的丰富层次的一种挑战与启示。现代数学和科学的发展中,许多理论都试图超越现有的极限概念,探索更为广阔的思想空间。
例如,模糊逻辑、非线性系统等新兴领域,常常意味着我们要走出传统的极限思维,去适应复杂性和不确定性。从不存的极限中汲取灵感,研究者们能够建立更新的理论框架,更深入理解自然界的运行规则。这种积极的态度也能够其他学科中引发新的思考,激励人们面对复杂问题时更加创新与包容。
结语
极限不存的现象是数学世界中的一个深刻主题,它引发了我们对未知领域的探索和对复杂性的理解。面对这样的情境时,我们不应抱怨或困惑,相反,应当知识探索的契机,促进思维的开放与转变。不断追寻和理解那些“不存”的极限,我们将获得更加丰厚的智慧,推动科学和人类思想的发展。
云作文原创内容,未经允许不得转载。